Figure 1
A Gaussian wavepacket incoming from the left hits a potential wall. The mean energy of the wavepacket is E=1.2 V0, i.e., it has enough energy to travel across the wall. Position x is given in units of ℏ/√(2 m V0)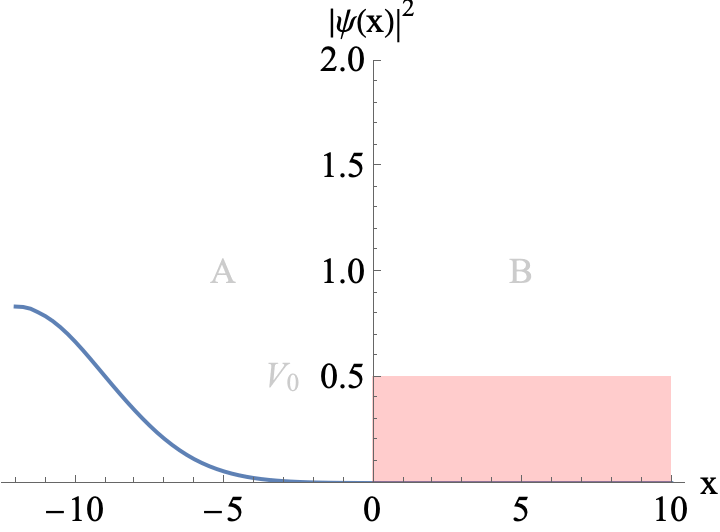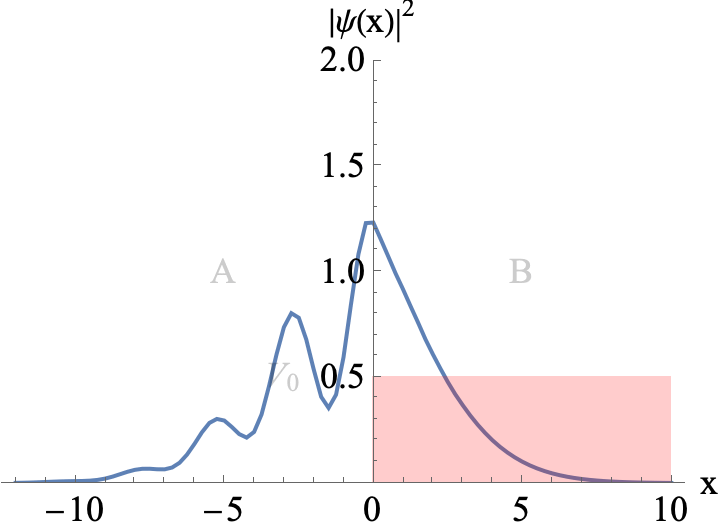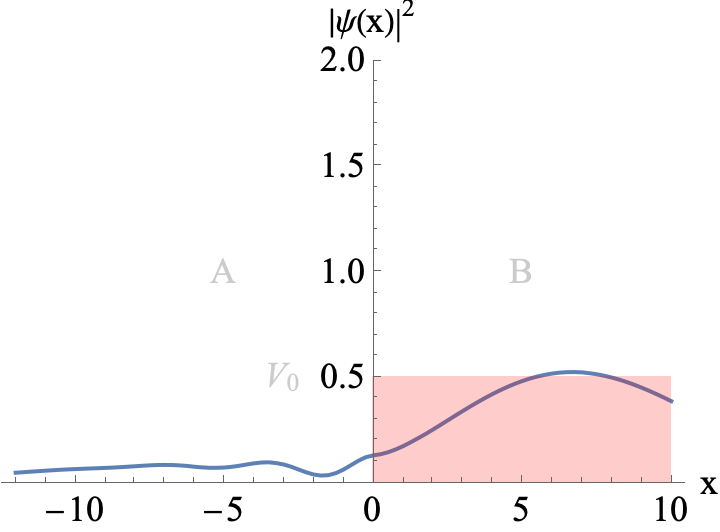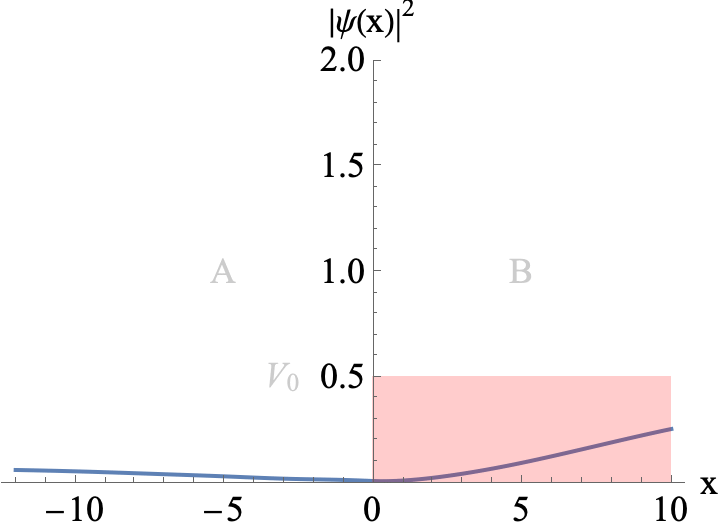
Figure 2
A Gaussian wavepacket incoming from the left hits a potential wall. The mean energy of the wavepacket is E=0.8 V0. A classical particle would be fully reflected by the wall. Parts of the wavepacket can leak into the classically forbidden region (skin effect)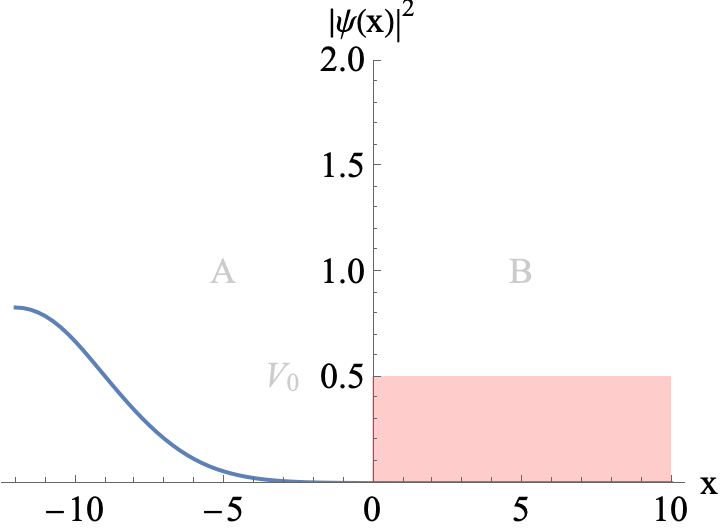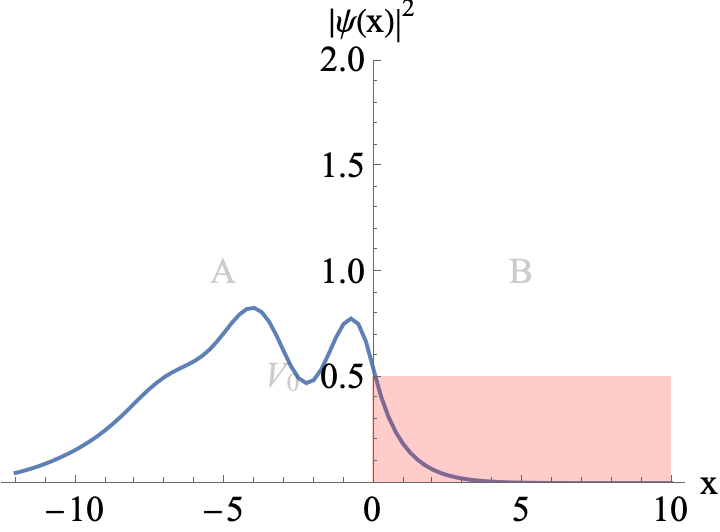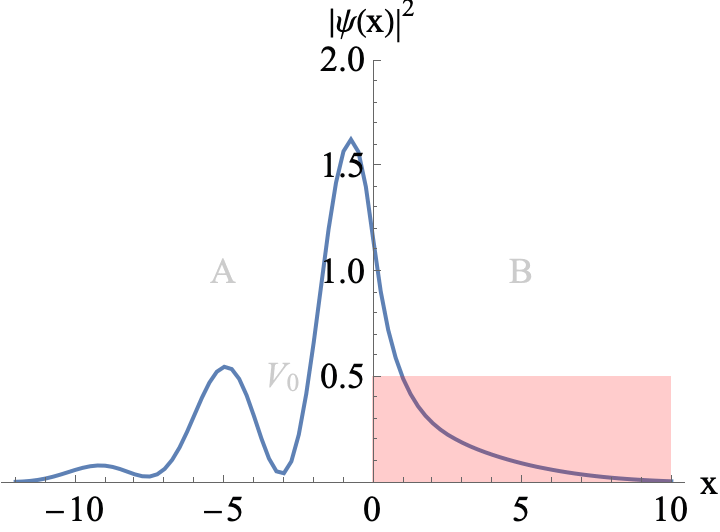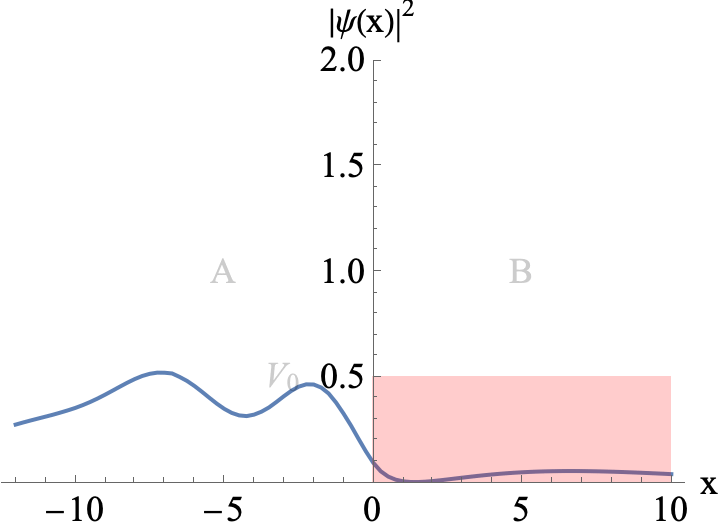
Figure 3
A Gaussian wavepacket incoming from the left hits a potential barrier of width L. The mean energy of the wavepacket is E=1.2 V0. You can see interference between incoming and reflected parts of the wavepackets when L is a multiple the de Broglie wavelength of a partial wave. 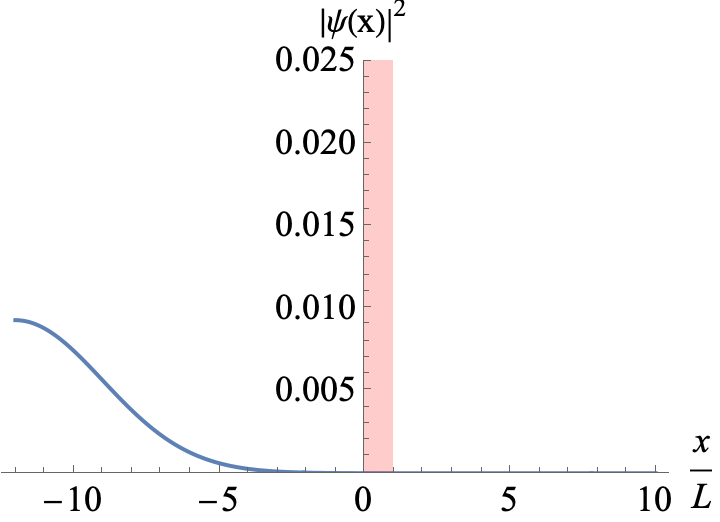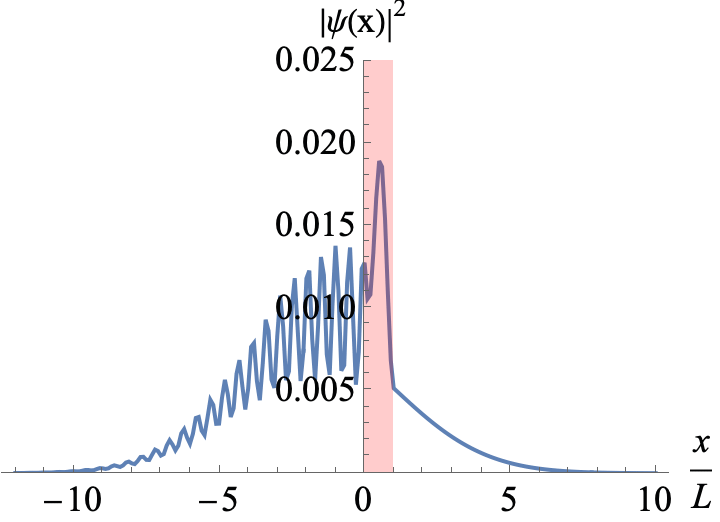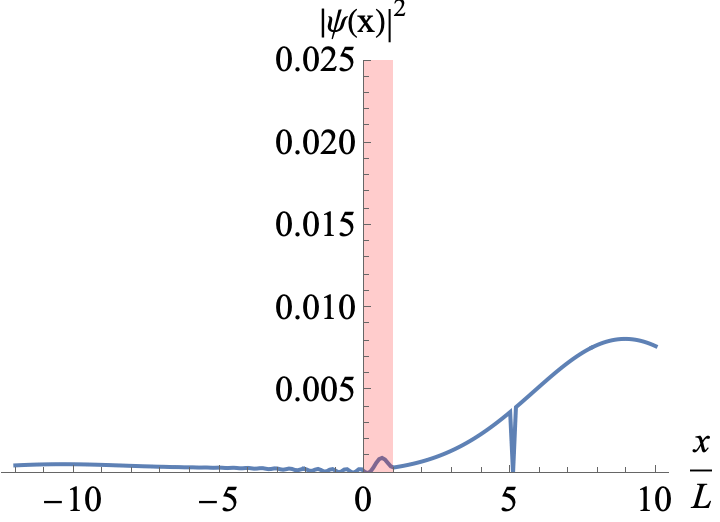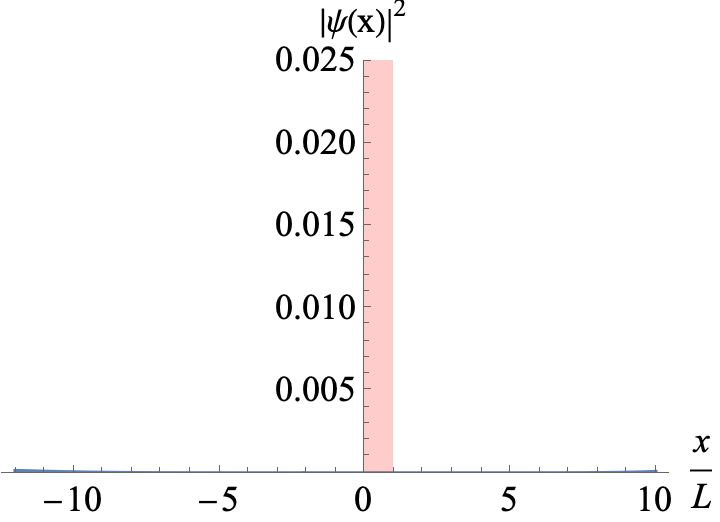
Figure 4
A Gaussian wavepacket incoming from the left hits a potential barrier of width L. The mean energy of the wavepacket is E=0.93 V0. S small part of the wavepacket is transmitted. This is quantum tunnelling 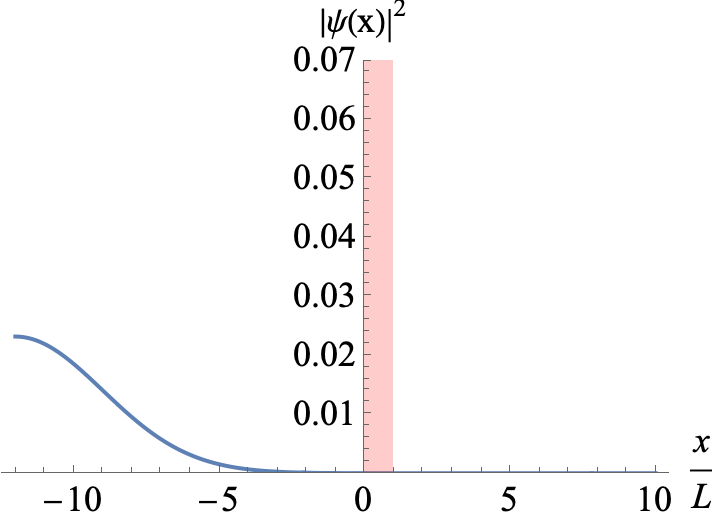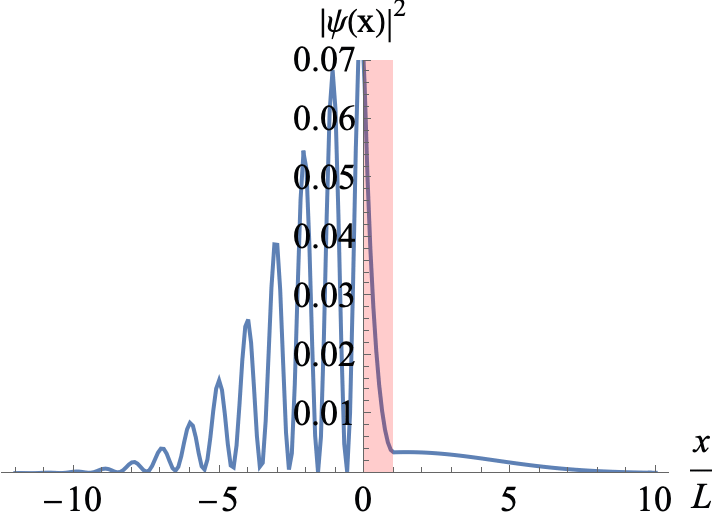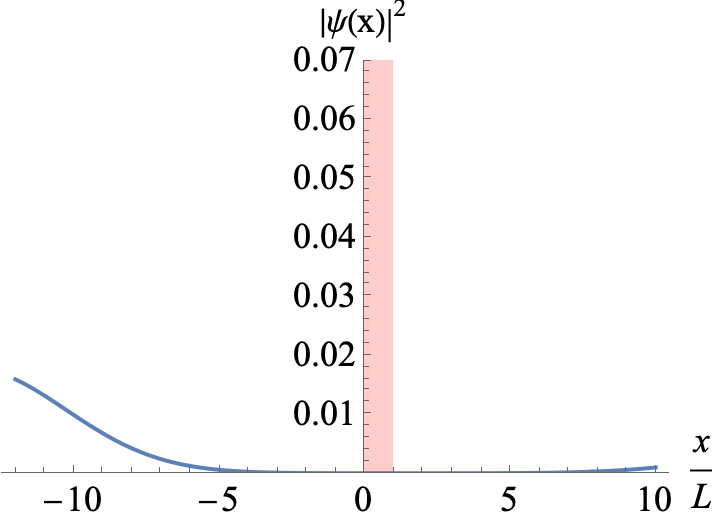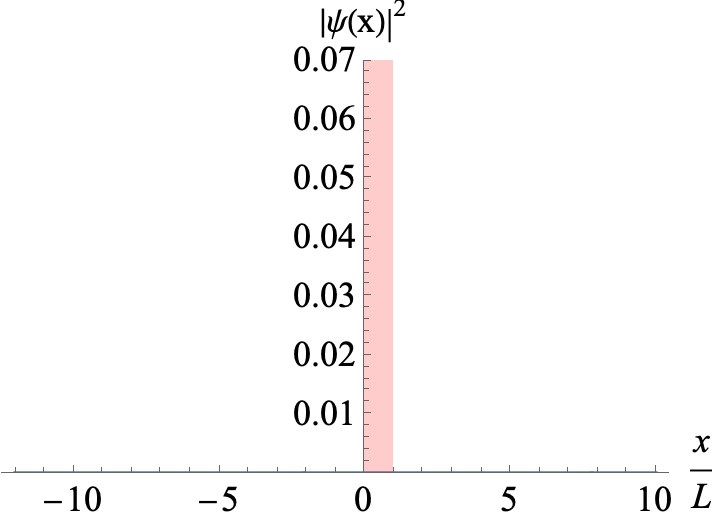
Contact
2052 Nasso Family Science Centre
5009 Chapel Square
Antigonish NS B2G 2W5
Canada

